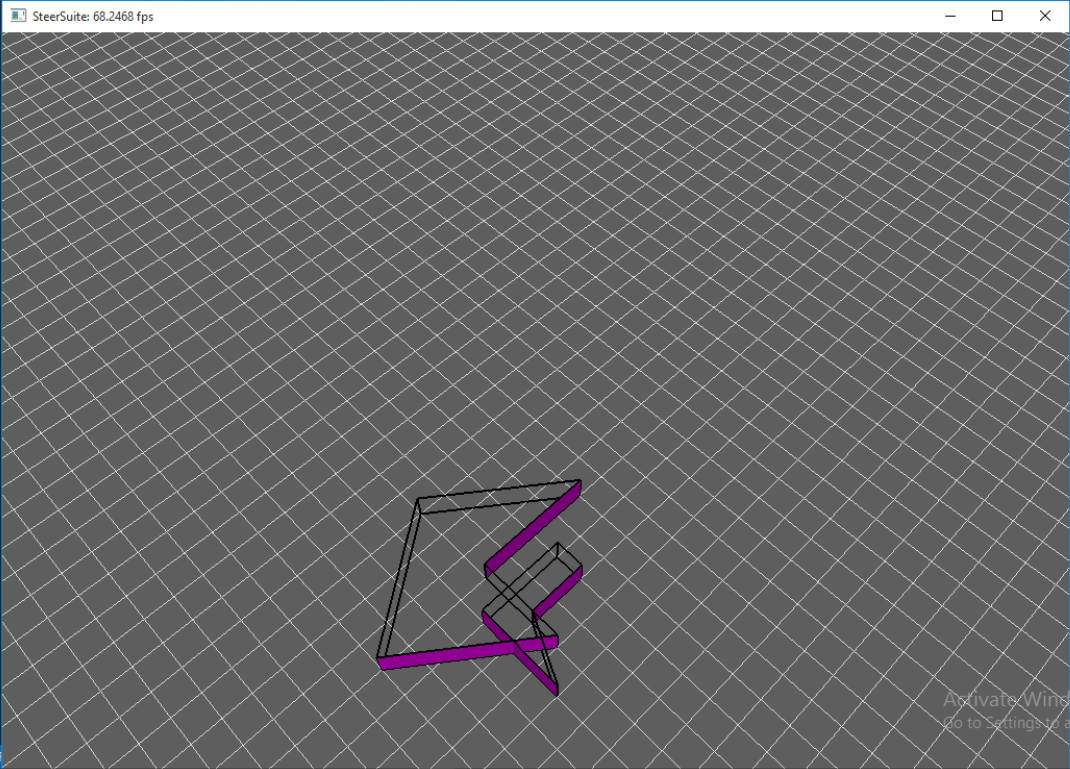
Description
Implementation
Polygon Triangulation via Ear Clipping
What is an ear?
An ear of a polygon is a vertex determined by its two neighbors. Let's say we have vertex p and its neighbors are (p+1) and (p-1).
p is an ear if the diagonal from (p+1) to (p-1) lies within the the polygon. If the diagonal lies on an edge of the polygon, it's not considered an ear.
How do you find them?
We get go through each point and get the midpoint between its two neighbors. If the midpoint is in the polygon, then you know that that point is an ear. We also tested if the midpoint was a point of the shape. In which case, the point is not an ear. We then push the point onto the queue of ears.
How do you triangulate?
We take the first ear in the queue and retrieve its neighbors. We construct a triangle out of the three points and store it in a vector. Afterwards, we remove the point wherever it's found. The neighbors that share the point get relinked to each other. Then we dequeue the ear and update the ears queue by going through the modified polygon to find new ears.
How do you detect collisions with GJK?
This was the simplest part of the entire process. After triangulating the shapes, we test each triangle from shapeA with each triangle from shapeB. If there two triangles are colliding and GJK detects it, the process stops and returns true.
Resources
The Two Ears Theorem
Triangulation by Ear Clipping
Triangulation
Pictures
Part D
$ ./steersim -testcase polygons3 -ai collisionAI
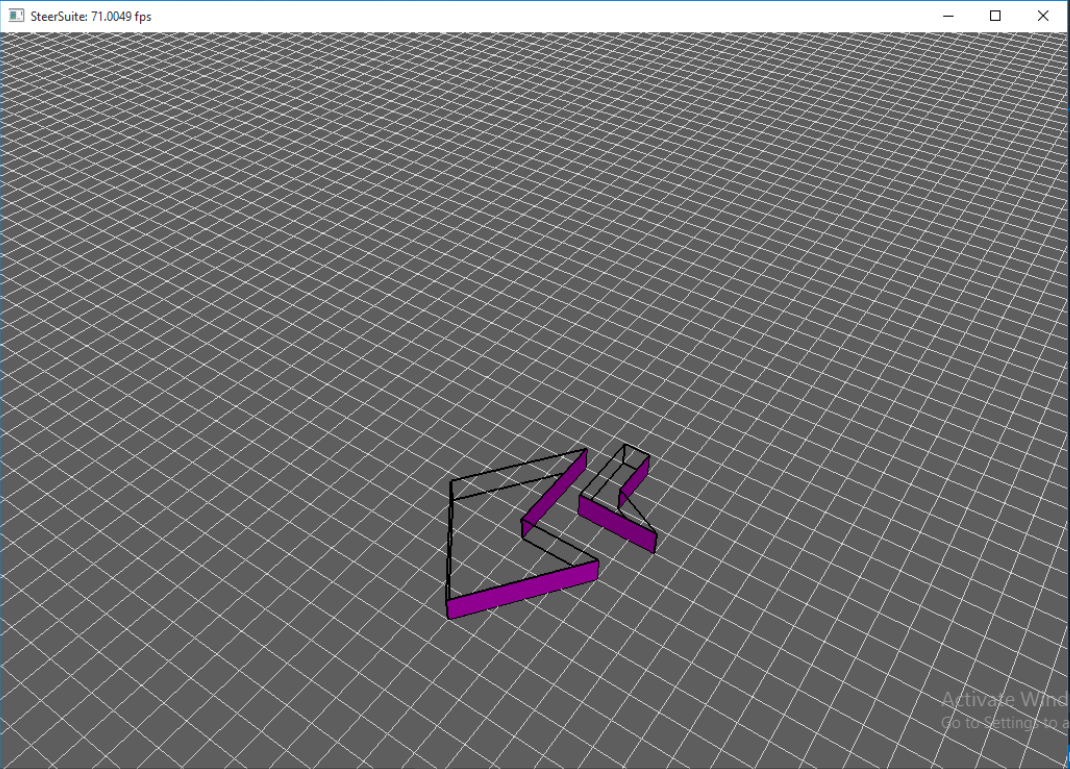
Part D (Modified polygons3 to have collision)
$ ./steersim -testcase polygons4 -ai collisionAI